树模型
文章目录
树模型
在各种机器学习的算法中,树模型可以说是最贴近于人类思维的模型,一切的树模型都是一种基于特征空间划分的,具有树形分支结构的模型。举个直观的例子:决策树。
决策树
决策树可以说是树模型中最基础,也是最有名的模型,它可以被认为是一堆条件判断的规则集合。
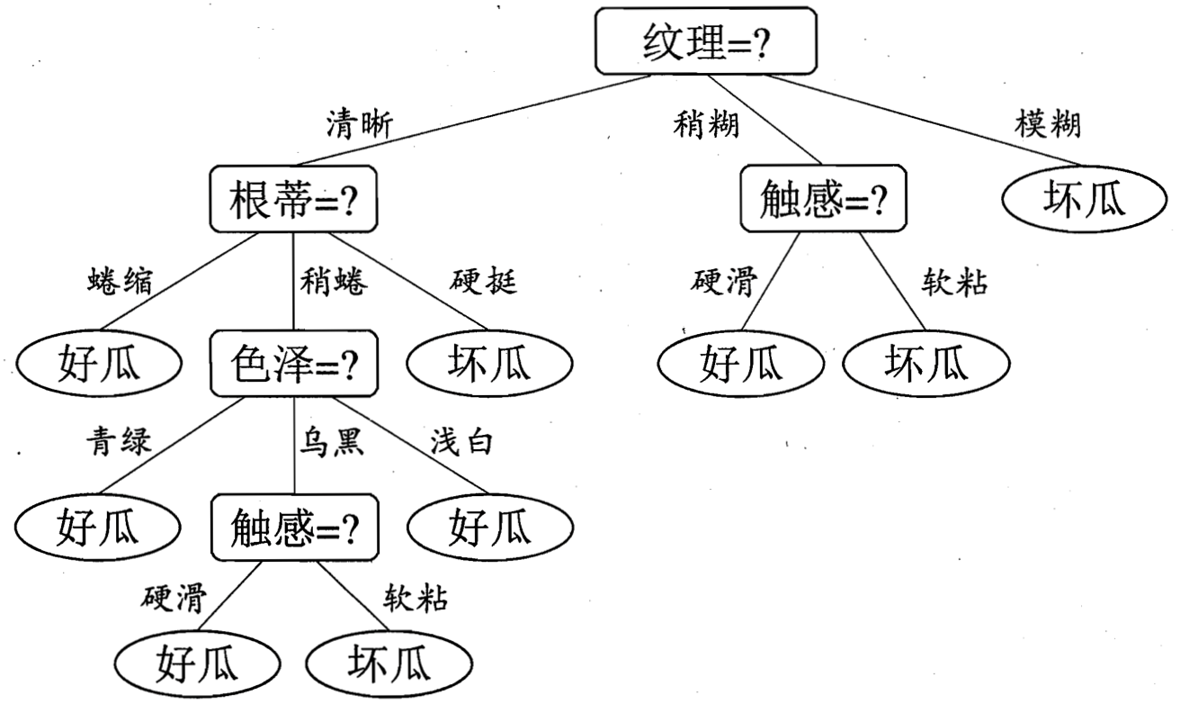
那么就像是这张图,去指导我们究竟应该如何去挑选一个好的西瓜:
- 首先,我们可以看它的纹理。如果纹理模糊,则是坏瓜。但如果纹理只是稍显模糊呢,那我们还需要去感受一下它的触感,那些摸起来硬滑的的才是好瓜;而摸起来有点软粘的瓜就坏了。
- 但其实,我们买瓜的时候,大多数瓜的纹理都是蛮清晰的,那么这个时候呢,我们就可以去看一看瓜蒂,如果瓜蒂蜷缩呢,就是好瓜;如果瓜蒂硬挺,就说明这个瓜比较老了,那它也是坏瓜。
- 但面对那种稍微蜷一点的呢,那我们还要去看它的色泽,青绿或浅白的都是好瓜。但如果是乌黑的呢,那我们又要去看它的触感了,硬滑的是好瓜,软粘的是坏瓜。
那么,如果这时候我买了一个西瓜,它的纹理是清晰的,瓜蒂是硬挺的,那我们就可以根据这张图,立马就知道,这是一颗坏西瓜了。
所以其实这张图呢,基本上就可以算作是一棵决策树了。
大家可能会觉得,决策树模型怎么这么简单呀,就是人类的正常思维嘛。的确,决策树模型的原理就是这么简单。但是,为什么我们刚才要说,这张图是基本可以算作决策树呢?是因为其中的判断条件并没有被量化,比如,纹理清晰,那究竟什么样算是清晰?还有,这个色泽青绿,这个青绿究竟是个什么样的颜色呢?那么,哪怕抛开这些量化问题,在决策树的原理当中,其实还有几个问题,是我们需要上升到理论的高度去解决的:
- 比如这棵选瓜的决策树,西瓜的特征由纹理、瓜蒂、触感、色泽,甚至还有没被写上去的敲击声,像我们平常就会通过敲击声去判断瓜的好坏嘛;还有像是瓜脐部是否凹陷,这也是我们平常判断瓜好坏的重要特征。但这么多特征,我们究竟应该选择哪个特征去划分特征空间,建立节点呢?这就是
特征选择和决策树生成的问题。 - 还有,我们通过递归去划分特征空间,从而建立决策树的方式,很可能会导致过拟合的问题。一般来说,这就需要我们对决策树进行剪枝。那么如何剪枝,这其实也是一个需要我们思考的问题。
特征选择及决策树生成
ID3算法
那么,我们首先来看特征选择问题。
如何选择一个特征进行划分,其实相当于是在讨论,用哪一个特征去划分特征空间,可以最有利于我们的分类,也就是说,划分之后的子集要尽可能地纯,尽可能地属于同一类别,换言之,就是降低了子特征空间的无序程度,也就是熵。
这边插一嘴哦,熵其实是一个物理概念,它指的是一个系统的无序程度。有这么一个说法哦,就是说一个封闭的系统,它永远都是趋向于熵增的。而这个熵增是什么呢?就好比是热水变冷,温差消失,原先有温差,代表能量在一个地方聚集,这个就是有序的,只有有序才能聚集;而最后温差消失了,系统每处温度都一样,这时候其实是无序的,大家都各自为政,一团散沙了嘛。像我们现在的宇宙是在膨胀的嘛,有一种学说是说宇宙膨胀的尽头就是热寂,到那时宇宙各处温度都一样,也不会再有做功,不会再有变化,这个就是热寂。所以,我们要想打破热寂,就必须要积极的引入外部因素,激活组织,当然了,这个就是管理学的范畴了,也就不展开说了。
那我们回归正题,既然熵表示的是无序的程度,它就肯定是和变量的分布有关系的。于是,我们假设某个特征$X$,当它为$x_i$时的概率,是$p_i$:
$$ P(X=x_i) = p_i $$
于是,我们就可以把变量$X$的熵定义为:
$$ H(X) = -\sum_{i=1}^n p_i log p_i $$
这边的$p_i$就是当$X$取值为$i$时侯的概率。
那么,数据集$D$,它的熵就可以表示为: $$ H(D)=-\sum_{k=1}^K { {|C_k|}\over{|D|} }log_2 { {|C_k| }\over{|D|} } $$ 在这里,我们假设数据集$D$有K个标签类别,那么$|C_k|$表示标签类别$k$的样本个数,而底下的分母$|D|$就表示样本总数,所以标签类别$k$的频率就是${|C_k|}\over {|D|}$了。为什么这边要强调是频率哦,是因为标签真正的概率很难获取,所以一般我们计算时使用它在数据集中出现的的频率,来代替它的概率,也就是用样本个数除以样本总数。
所以,特征$A$对数据集$D$的经验条件熵$H(D|A)$,我们就可以定义为: $$ H(D|A)=\sum_{i=1}^n { {|D_i|} \over {|D|} } H(D_i) = - \sum_{i=1}^n { {|D_i|} \over {|D|} } \sum_{k=1}^K { {|D_{ik}|} \over {|D_i|} } log_2 { {|D_{ik}|} \over {|D_i|} } $$ 我们先看前半个式子,我们假设数据集$D$被特征$A$划分成了$n$个子集,所以它的条件熵就是每个子集的概率乘以这个子集的熵。那么,我们把这个$H(D_i)$给展开,就是我们看到的第二个式子了。
那么,到此为止,一个给定数据集的熵我们就可以计算出来了。但是,我们选取一个特征来划分数据集,所要比较的其实是划分前后熵的变化,所以,我们就可以定义$ 信息增益 $为数据集$D$的熵,与 在给定特征$A$的条件下数据集D的熵之差,即: $$ g(D,A) = H(D) - H(D|A) $$
所以,我们最终要选取的特征,也就是给定哪个特征$A$,它的信息增益最大,那它就是我们要用来划分数据集的那个特征。
而这种算法,就是所谓的 ID3算法。也就是,每次选取信息增益最大的特征进行划分,递归地执行上述的步骤,直到所有特征的信息增益很小,或是在叶子节点熵没有了特征为止。
C4.5算法
而我们刚才说的信息增益,其实有个小问题,就是它会偏向于去选择取值种类较多的那个特征。比如,编号 这个特征,它里面所有的取值都是唯一的,那么一旦选择这个特征进行划分的话,将会产生n个子集,而每个子集中只有一个样本,所以它的条件熵为0 。 $$ H(D|A) = \sum_{i=1}^n { {|D_i|} \over {|D|} } H(D_i) = \sum_{i=1}^n {1\over n} H(D_i) = - \sum_{i=1}^n {1\over n} { {1\over1} log_2 {1\over1} } = - \sum_{i=1}^n {1\over n} {log_2 {1} } = 0 $$ 则,它的信息增益就是数据集的熵,取到了最大值。 $$ g(D,A) = H(D) - H(D|A) = H(D) - 0 = H(D) $$
然而,用这种特征去划分特征空间,也就相当于是说:你告诉我编号,我立马就能知道它的最终分类。但其实在预测时,所见到的编号都是新的,也就是说编号这个特征在实际预测时,是没有用处的,所以选择这种特征,划分的效果就非常差了。
为了解决这个问题,C4.5算法就使用信息增益比,来选择特征。 $$ g_R(D,A) = {g(D,A)\over H_A(D)} $$
即,信息增益比$g_R(D,A)$,为其信息增益$g(D,A)$与数据集D关于特征A的熵$H_A(D)$ 之比(之前是把标签取值当作变量,$H_A(D)$这个是把特征A的取值当作变量)。这样,也就相当于,是在信息增益的基础之上乘以了一个惩罚参数。
而C4.5算法其余建立树的步骤,与ID3算法一样。
但是,改成信息增益比之后,其实还有一个问题,就是用特征熵的倒数作为惩罚项,在一些极端情况下,会偏向于去选择种类较少的那个特征。所以,一般我们在具体实现时,往往并不是直接选择 信息增益比 最大的那个特征,而是先找出 信息增益 高于平均水平的那些特征,然后再从这些特征中去选择 信息增益比 最大的那个特征。
这边再讲一个小插曲哦,其实,ID3算法和C4.5算法都是同一个人发明的,他叫做 罗斯 昆兰。在1978年的时候,罗斯昆兰去斯坦福大学访问,正好有个项目是要写一个程序,来判断国际象棋是否会在两步之后被对方将死,而在这个项目当中,昆兰最重要的工作就是引入了信息增益准则。所以在1979年的时候,昆兰就把这部分工作给整理出来发表了,这就是ID3算法的由来。结果,ID3算法就掀起了决策树研究的热潮,一时间ID4、ID5的名字就迅速被其他研究者给占用,所以等到昆兰自己提出ID3的改进算法的时候,就已经没有名字可用了,于是乎,昆兰就给自己的改进算法起名叫“第4.5代分类器”,也就是我们刚才讲的C4.5算法。所以说大佬就是大佬,一下子就是“第4.5代分类器”,意思就是,之前别人的那些就都是旧版的了。
CART算法
分类与回归树(classification and regression tree, CART)模型,该模型假设决策树是二叉树,其内部节点相当于是在做一个二元的是否的判断,所以,CART算法就不像是之前的算法那样可以按照特征的取值种类,划分出多个子特征空间。那么,我们就必须要去讨论,CART算法究竟要选取特征的哪个取值,去做是否的判断划分呢?
首先,CART算法是对回归树使用平方误差最小化准则,而对分类树使用基尼指数最小化准则,来进行特征选择,从而生成二叉树的。 $$ Gini(p) = \sum_{k=1}^Kp_k(1-p_k) = 1 - \sum_{k=1}^K(p_k)^2 $$
我们以基尼指数为例,这个就是基尼指数公式,其中的$p_k$就是样本属于$k$这个类别的概率,那么$(1-p_k)$就是这个样本被分错的概率。所以,基尼指数其实就等于$样本被选中的概率 * 样本被分错的概率$,那么,当我们选择基尼指数来进行特征划分的时候,其实就是在使得,划分之后的,子特征空间里的样本,被分错的概率在逐步地减小。 $$ Gini(D,A)={ {|D_1|} \over {|D|} }Gini(D_1) + { {|D_2|} \over {|D|} }Gini(D_2) $$ 所以,当我们按照特征$A$,把数据集$D$划分为子集$D_1$和$D_2$之后,它们的条件基尼指数,其实就是,子集$D_1$在数据集$D$中的概率,乘以它的基尼指数,再加上子集$D_2$的概率乘以它的基尼指数。那么,我们只需要去找到最小的条件基尼指数,就能够找到哪个特征是数据集的最佳划分点了。
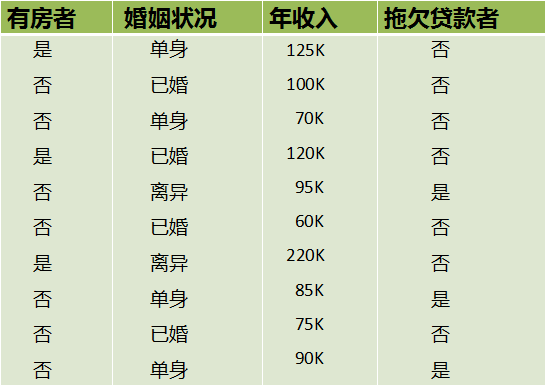
说了这三种特征选择的方法,可能大家还是有点模糊哦,我们正好用这个基尼指数来看个例子。在这张图中,有三个特征,是否有房、婚姻状况和年收入,还有一个标签,是否是拖款者。
那么,因为婚姻状况的取值有三种,所以我们来看一下如果按照婚姻状况来划分数据集的话,划分之后的基尼指数是什么样的:
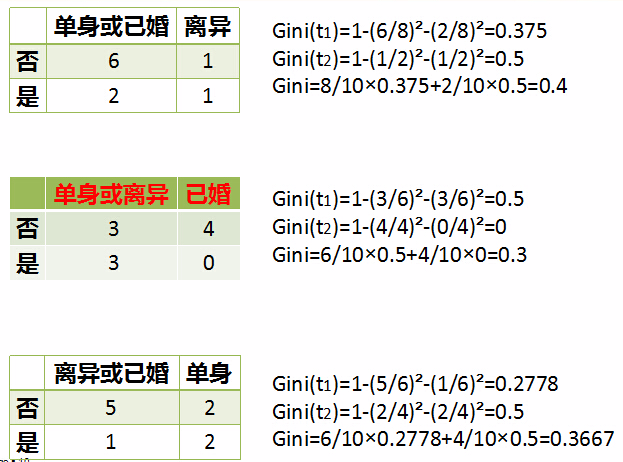
按照是否离异来划分,离异这个子集离有2个样本,一个不是拖款者另一个是,所以$Gini$指数是$t2$这个式子。而非离异的子集离有8个样本,6个不是拖款者,2个是的,所以式子就是$t1$这个式子了,最后再按照每个子集的概率加权相加即可。
也就是说,我们按照该特征中每种取值的划分情况,单独算出每个子集的$Gini$指数,再加权相加。
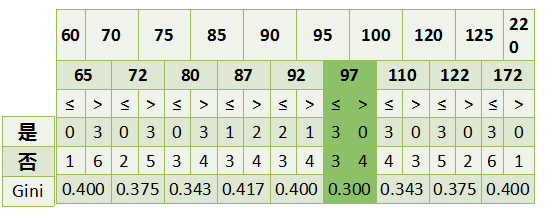
而如果是连续值的特征,那么我们就把相邻两个取值的均值作为分裂点,去计算每个分裂点的$Gini$指数。比如说该例子中,这个特征的取值是第一行60、70、75等等,那它们的分裂点就是相邻的取值的均值,也就是第二行65、72、80这个。然后再算出每个分裂点的$Gini$指数,取最小的即可。
决策树的剪枝
那么接下来我们来讲一下决策树的剪枝。
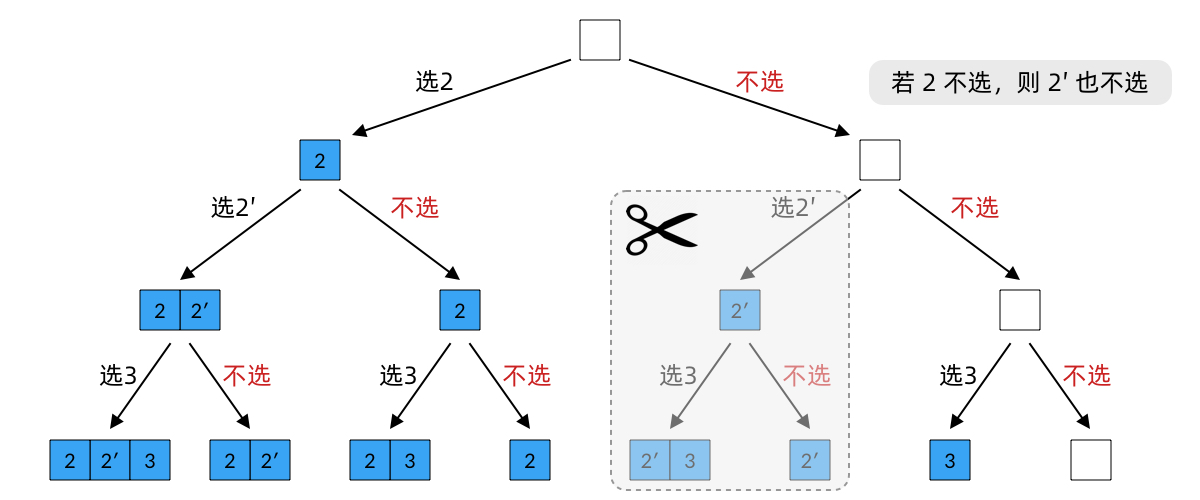
我们之前说到过,建立决策树的时候,我们是采用递归的方法,一直建立到不能继续了为止。但是,这样产生的树往往泛化能力比较弱。所以,我们需要考虑树的复杂度,对决策树进行简化,从而提高泛化能力。
而剪枝一般分为两种,一种是 先剪枝 ,另一种是 后剪枝 。
所谓 先剪枝 ,就是,在构造的过程中,当某个节点满足剪枝条件时,就停止此分支的构造。举个最简单的例子,比如我们可以额外的再加一个验证集,那么我们就可以在这个验证集上,去计算划分前后的正确率,如果正确率降低了,那么就禁止这个节点的划分。
而 后剪枝 ,则是先构造一棵完整的决策树,然后再通过某些条件,去遍历整棵树,进行剪枝。 $$ C_\alpha(T) = \sum_{t=1}^{|T|}N_tH_t(T) + \alpha|T| $$
具体的条件呢,就是用这个决策树的损失函数$C_\alpha(T)$。其中,$t$为决策树$T$的叶子节点,$N_t$为该叶子节点的样本个数,而$H_t(T)$为叶子节点$t$的熵,最后的$\alpha$就是正则化系数。
所以,在有了这个式子之后,我们就可以整体地来讲一下剪枝的思路了:
首先,我们计算出每个节点的熵,然后递归的从叶节点向上尝试回缩,从而计算出回缩前后树的损失函数;
那么我们最后所得到的呢,就是损失函数最小的那棵决策树了。
集成学习
但是,光有一个决策树模型去解决问题,可能还不够好。所以,我们就需要一种可以集合多个模型来共同解决问题的方法,这个就是集成学习。

从这张图可以看到,所谓集成学习(ensemble learning) 是通过构建并结合多个学习器,来完成任务的一种方法。那么,为什么这边写的是个体学习器,而不叫其他的名字呢?其实,如果我们的集成方法当中,只包含同种类型的个体学习器,那么这种集成就可以叫做“同质集成”,其中的学习器也可以叫做“基学习器”。而如果我们的集成方法当中包含了不同类型的学习器,比如说同时包含了决策树和神经网络,那么这种集成就可以叫做“异质集成”,而其中的学习器则叫做组件学习器,或者干脆就叫做个体学习器。所以,我们这边写做 个体学习器,就比较通用了。
那么,集成学习的理论基础呢,是Schapire这个人在1995年,证明了 强可学习与弱可学习是等价的,这么一个概念。所谓弱可学习就是,这个模型的正确率只比随机猜测要好一点点。而强可学习呢,就是指这个模型的效果会非常的好。而这个人证明了,强可学习和弱可学习,是等价的,意思就是说,不管所采用的方法是难还是易,总之我们一定可以找到一种集成方法,去把弱学习器给变成强学习器,而弱可学习器是非常容易获取的。

但是,按照我们一般的感觉,好像会认为,如果简单地把一堆学习器,相加求平均,那么它的效果应该是比最差的要好一点,但是比最好的要差一点。

举个直观的例子,就像是这幅图。我们假设集成方法采取的是最常见的投票法,即少数服从多数。那么,在第一幅图中,每个分类器的正确率都是66%,并且正巧,每个分类器分错的都是不同的类别,那么根据投票法,我们最终的集成器,它的正确率可以达到100%。而在第二幅图中,虽然每个分类器的正确率也是66%,但是他们都错在了同一个类别上,所以集成之后并没有提高正确率。而这最后一幅图,每个分类器的正确率只有33%,虽然他们都对在了不同的类别上,但投票之后,整个集成方法的正确率却是0%。
所以,回到之前的问题,我们究竟应该怎样做才能得到比最好的学习器还要好的集成效果呢?这个答案其实是,我们的每个个体学习器要“好而不同”。也就是说,每个学习器都不能太差,并且要有所差异,才能集成出一个更好的结果。
那么,具体有哪些集成方法呢?
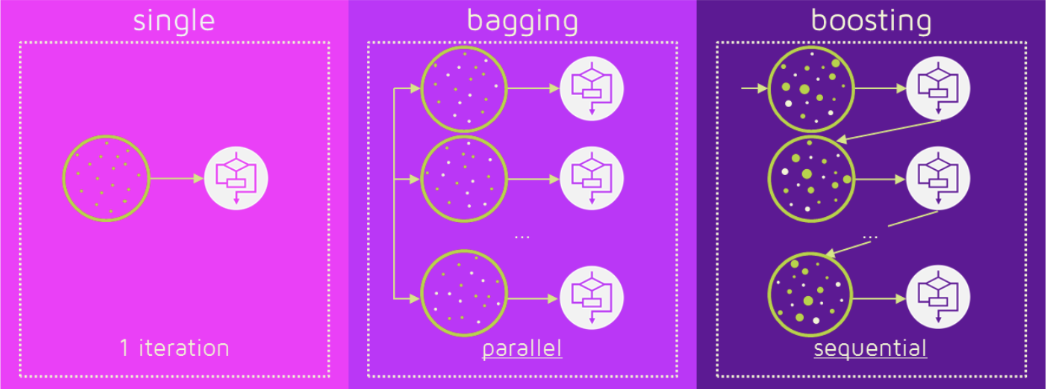
我们按照个体学习器之间是否存在依赖关系,可以分为两种:
- 第一种是个体学习器之间不存在强依赖关系,它们可以并行的去生成。这一类的代表方法是bagging和随机森林算法。
- 而第二种则是个体学习器之间存在强依赖,即后一个学习器的构建需要依赖前一个学习器的结果,它们是串行构建的。这种类别的代表方法是boosting算法。
bagging
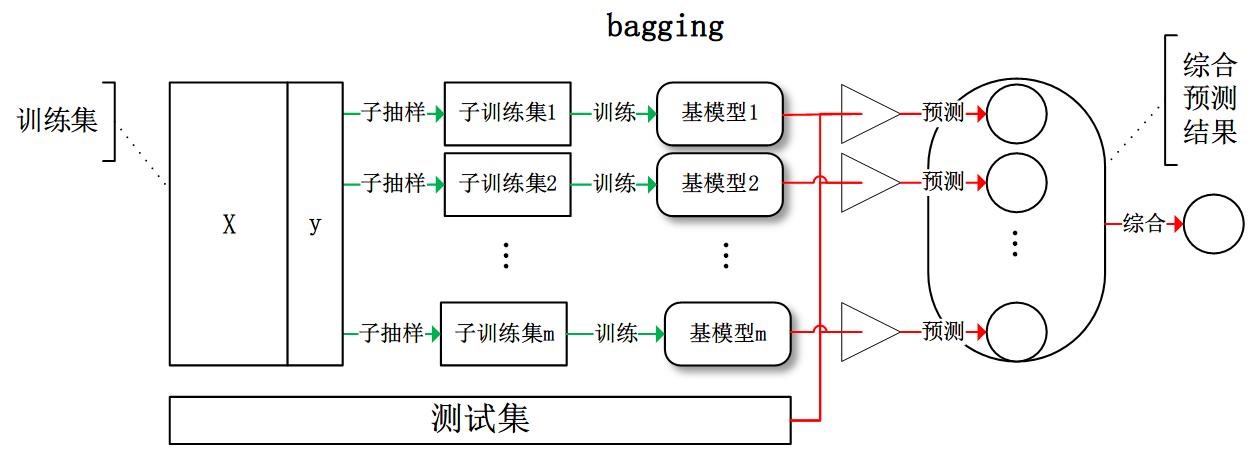
我们现在来讲一下,可以并行构建的bagging算法,Bagging (bootstrap aggregating),其实是这两个单词的简写。而这个 bootstrap ,也被称为自助法,就是一种有放回的抽样方法。所以,bagging算法其实就是利用这个方法,从整体数据集中有放回的抽样,从而得到N个子数据集。这样,我们就可以在每个子数据集上学习出一个基模型,从而综合出最终的预测结果。具体的综合方法就是,比如像是分类问题,我们就可以采用N个模型投票的方式来进行综合;而回归问题,则可以采用N个模型求平均的方式去得到。
这边再插一嘴哦,就像是平常做深度学习时候,我们所使用的dropout,也就是以一定概率随机的使一部分神经元暂时停止工作嘛,而这种方式,其实也就相当于是一种轻量版的bagging,也就相当于是在训练多种模型嘛。
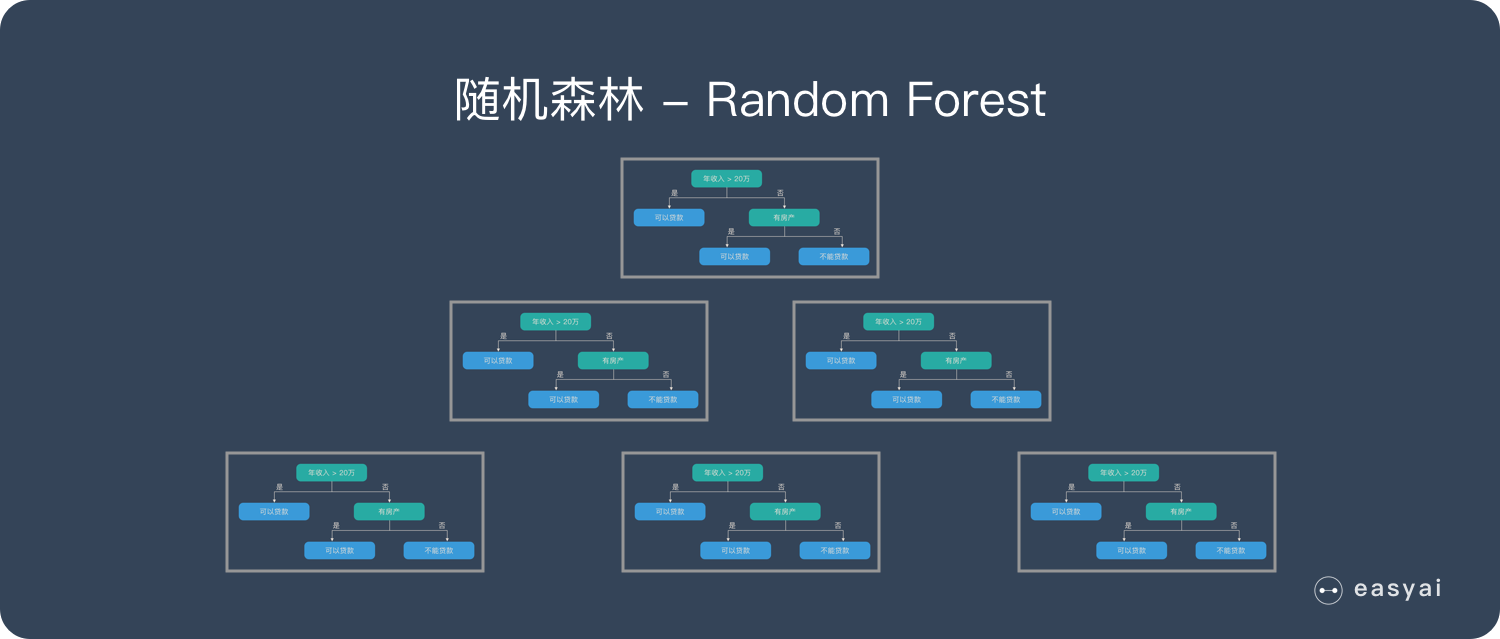
另外,像是随机森林算法,它也可以算作是bagging的一个变种。随机森林其实就是用随机抽样的方法,去生成N个不同的数据集,从而建立N棵决策树。并且因为是并行集成方法嘛,所以在随机森林中不同的决策树之间是没有关联的。而且在建立决策树时,并不是选取最优的那个特征来划分特征空间,而是先随机选取k个特征,然后从这k个特征中选择最优的那个特征进行划分。这种方法就相当于是,原先的bagging仅仅是样本的扰动,而随机森林算法不光是样本的扰动,还有属性的扰动,这样就可以最大程度的提升最终集成的泛化效果,也就达到了我们前面所说的“好而不同”。
提升方法(boosting)
下面我们来讲一下这个boosting方法,它其实就是用前一个基模型的输出结果,与真实值之间的差,也就是残差,去改变训练数据的概率或权重分布,从而训练出一系列的弱分类器。
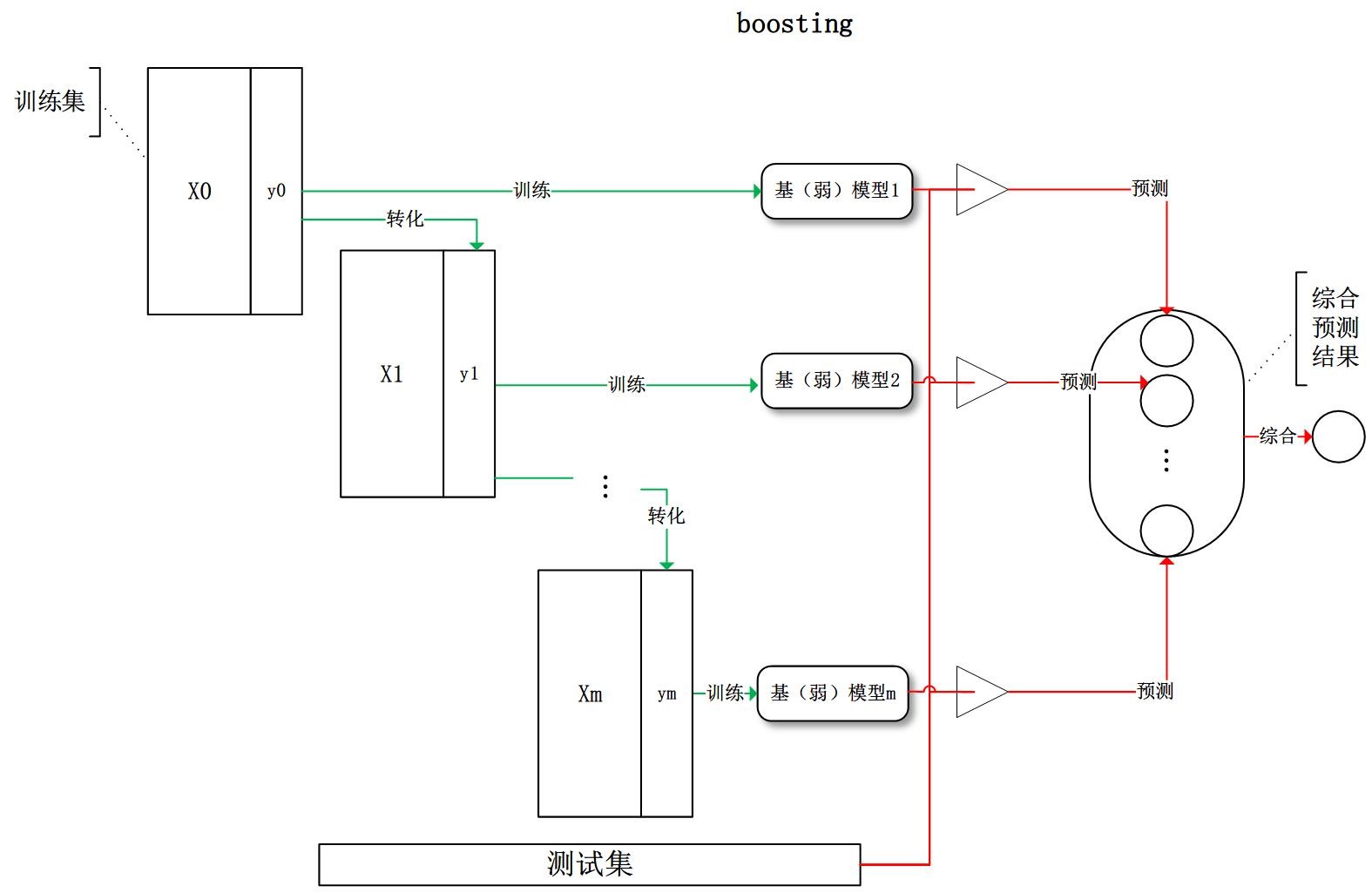
而我们刚才说的残差,其实应该是预测值与观察值之间的差,与不是与真实值之间的差。只不过在这里,并不需要去区分的这么细,所以一般来说,残差也就等于误差了。
而我们看这个误差的公式:
$$
误差=偏差+方差+噪声
$$
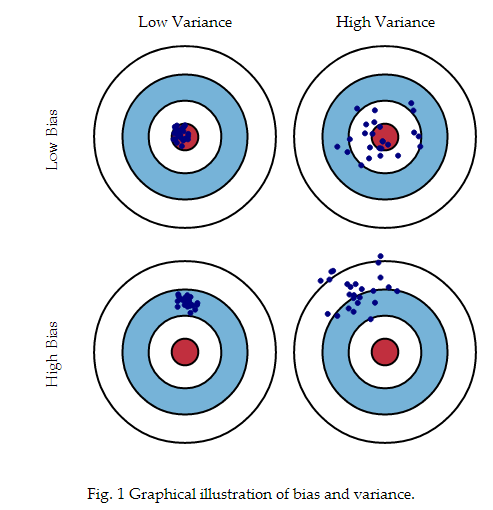
误差等于偏差加方差加噪声嘛。那么,为什么要说公式 呢?是因为,当我们训练一个模型的时候,我们肯定是要以降低它的误差为目的的嘛。但是噪声我们不好控制,所以方便下手的就只有偏差和方差了。那么,究竟什么是偏差,什么是方差呢?大家可以看这幅图哦。
这边第一行是低偏差,第二行是高偏差。大家可以看出来,低偏差它的预测值的中心点离真实值比较接近,而高偏差的话呢,预测值的中心点就离真实值比较远了。
而这边第一列是低方差,第二列是高方差。可以看出来,所谓方差就是指预测值的离散程度。低方差的时候,预测值就比较抱团。而高方差的时候,预测值分的就比较散。
而我们上一张所说的bagging算法呢,因为它是随机抽取的方法去建立的样本子集嘛,所以它每一个样本子集的分布都是近似的,那么一旦数据有偏差的话,bagging算法其实是不能够有效地降低偏差的。但是它的模型都是相互独立的嘛,选取的特征划分也是有所差异的,所以bagging算法可以在一定程度上降低方差。所以,当我们使用不剪枝的决策树,或是神经网络,这些容易受到样本扰动的算法作为基学习器的时候,bagging的效果就比较好了。
而我们前面所说的另外一个算法,也就是boosting算法,它其实是在不断地拟合残差,所以boosting算法实际上是在降低偏差;但是由于它的基模型之间是串行生成的,也就是说boosting的基模型之间是强相关的,所以,它并不能明显的降低方差。但其实呢,我们在具体实现的过程中,也有办法去降低方差,就是在目标函数中添加正则项,防止过拟合。
好,那么接下来我们来讲一个著名的,boosting的实现方法。
AdaBoost提升方法
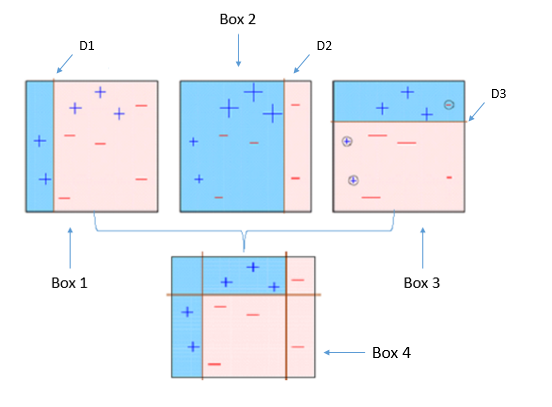
也就是这个,AdaBoost (Adaptive Boosting)提升方法,它是比较具有代表性的一种提升方法。它具体的做法是,提高那些被前一轮弱分类器错误分类的样本的权重,而降低那些已经被正确分类的样本的权重。那么这样一来,在上一轮分类器中没有被正确分类的样本,就可以在这一轮的弱分类器中,得到更大的关注。
而最终,AdaBoost会采取加权投票的方式,具体的就是,去加大误差率小的分类器的权重,而降低误差率大的分类器的权重,用这种方法去综合多个弱分类器的结果。
提升树
而提升树(boosting tree)算法,则是以决策树(分类树(最小化基尼指数)或回归树(以相邻节点的均值作为分裂点,去寻找平方误差最小的分裂点))为基分类器的提升方法,可以算作是AdaBoost算法的特殊情况。
梯度提升算法
我们前面提到过,其实boosting算法就是在不断地拟合残差。但是,当使用平方误差损失函数或指数损失函数的时侯,残差的求解比较方便,但是在使用一般的损失误差函数时,残差的求解就不是那么容易了。
所以,Freidman就提出了梯度提升(gradient boosting)算法。它主要思想是利用损失函数的负梯度,去近似求解残差。那么,我们的优化方向是沿着负梯度的方向前进的嘛,这个也就是梯度下降法了。
而在梯度提升算法Gradient Boosting中,最有代表性的就是GBDT(Gradient Boosting Descision Tree) 梯度提升决策树。
这个名字大家其实可以发现哦,其实这个GBDT,它里面包含了DT(Descision Tree)决策树、Boosting 提升方法(也就是用一组弱分类器综合成一个强分类器),和 Gradient Boosting 梯度提升方法(也就是用梯度信息对弱分类器进行加权),而梯度提升方法,其实就是用计算梯度的方式,去实现这个Boosting 提升方法。
xgboost
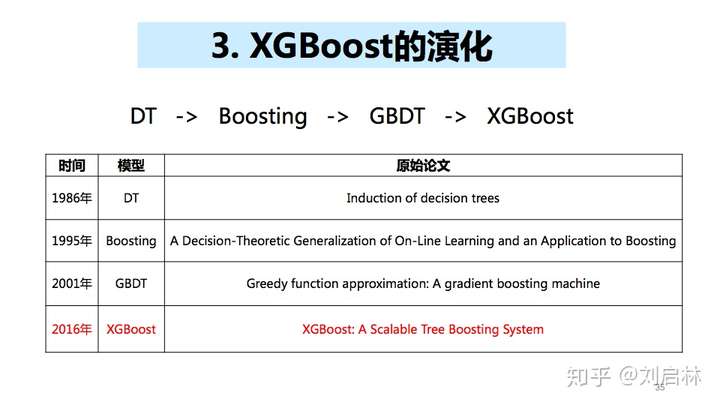
接下来就到了我们今天介绍的最后一个算法,XGBoost(Extreme Gradient Boosting),从它的名字就可以看出来,极致梯度提升,所以xgb其实是GBDT的一种高效实现,但是XGBoost同时也进行了许多的优化。
那么,xgb与gbdt主要的差别在于:
传统的GBDT在计算loss函数时,只使用了一阶导数;而XGBoost对Loss进行泰勒展开,取了一阶导数和二阶导数。这样就可以提高xgb的准确率。

同时,XGBoost还考虑了正则化项,包含了对复杂模型的惩罚,比如叶节点的个数、树的深度这些。那么这样就可以确保树的简单性,也就提高了泛化程度。并且我们前面说过,模型的预测精度由模型的偏差和方差共同决定,第一条的损失函数代表了模型的偏差,而想要方差小的话,则需要这个第二条,在目标函数中添加正则项,来防止过拟合。
此外,xgb还采用列抽样和并行处理等方式,提高了效率。
总结及与业务的结合
好,最后总结一下就是,树模型的本质其实是去改变样本集的权重或是概率的分布,从而将许多个体学习器的结果综合起来。那么,从这一过程我们其实可以看出,树模型其实更加适合于去处理异质化数据。什么是异质化数据呢?就是说比如数据不光有embedding这个特征,还有段落数、字数、图片个数等其他含义的特征。那么这种数据使用树模型时,往往就可以对数据特征关注得比较充分,模型效果也就比较好了。比方说我们的负面和优质模型。
这些模型,特别是优质模型,怎么去判断一篇文章的优质,它不光关注文章的语义信息(具体写的是什么),还要更加关注文章的结构信息(有几段,有多少图片等行文布局方面的特征),所以我们就可以把这些异质的特征,做好处理后,采用诸如xgboost、catboost这类树模型去解决问题。事实上,在我们的优质模型没有上线之前,运营要人工为每日精选栏目去挑选优质文章,这样挑选的数目少、人还累,而自从模型上线之后,就变为了由模型直接入库和人工审核的模式,节约了大量人力,可用的文章数目还多,获得了一致的好评。
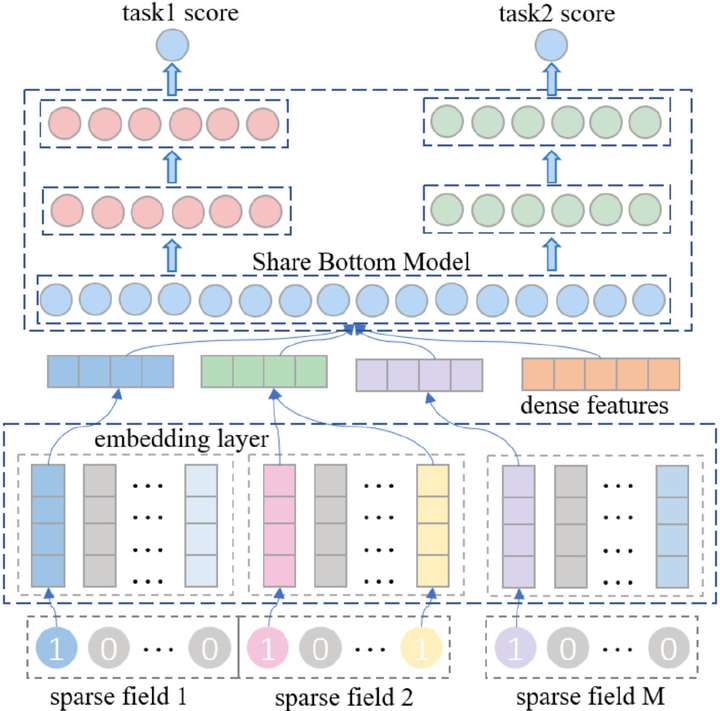
最后再说一点,其实对于同质数据的处理,比如像是分类模型,它就比较关注文章的语义信息,所以只要文章embedding就够了。那么我们现在所在研究的一个方向,其实就是用多任务、多输出的深度模型,比如底层我们采用bert做一个共享参数的embedding层,然后上面连接3个用于输出的子网络层,分别学习一、二、三级的分类信息。这种树状多任务模型结构的好处是,由于底层的参数被所有目标共享,所以大大降低了过拟合的风险;与此同时,不同目标在学习时也可以通过这些共享的参数进行知识迁移,从而利用其它目标学习到的知识帮助自己目标的学习,起到一个纠偏的作用。
而为什么有相关联性的多任务学习,可以提高模型总的正确率呢?是因为多任务学习,它其实是一种归纳迁移机制,其主要目标,是利用隐含在多个相关任务标签中的特定领域信息,来提高泛化能力。所以,多任务学习,一般是通过使用共享层,来训练多个任务目标,这样,多任务学习在学习一个问题的同时,就可以通过使用共享层的表示,来获得其他相关问题的知识。再举一个学习到其他相关知识的例子,就是为什么模型蒸馏可以让小模型,比起直接学习任务目标,模型蒸馏的效果要更好呢?有一种解释是说,因为模型蒸馏对齐的是中间层的输出,也就相当于是让小模型从原来的学习分类标签,变成了学习分类标签的概率分布,这样它所学习到的知识,比原先单纯的标签要多很多。这也就从另一个侧面解释了,为什么有相关性的多任务学习,往往可以提高模型总的正确率。
在我们实际的实验中,这种层次分类的多任务模型,的确比之前每层训练一个单任务的模型,指标有很大的提升。所以这个也是未来的一个演进方向。